Numbers – Concepts and Formulas for Aptitude

For scope of Placement Aptitude, we will restrict the topic to real numbers. Real numbers are of 2 types: rational and irrational

1. Definitions

Rational Numbers

A number which can be expressed in the form p/q where p and q are integers and q$ \ne $ 0 is called a rational number. For example : 6, -31, 73/2, -7/23 etc.
Between any two numbers, there can be infinite number of other rational numbers.
Rational numbers an be further be classified into two categories –
- Terminating Decimals
  - A terminating decimal is a decimal number that ends or terminates after a finite number of digits.
  - For example, the fraction 1/4 is equal to 0.25 in decimal form.
  - Non-Terminating but Repeating decimals
  - These decimals do not end but repeat a pattern of digits indefinitely.
  - For example, the fraction 1/3 has a decimal representation of 0.333…, where the digit 3 repeats infinitely.

Irrational Numbers

Numbers which are not rational but which can be represented by points on the number line are called irrational numbers.
Examples for irrational numbers are $ \pi , \mathrm{e} , \sqrt{2} , \sqrt{7} , \sqrt[4]{5} $ etc.
Between any two numbers, there are infinite number of irrational numbers.
Any non-terminating non-recurring decimal is an irrational number.

Integers

Integers are a special type of rational numbers which we all are familiar with:

Integers are whole numbers, including both positive and negative numbers, as well as zero.
All integers are rational numbers. The set of integers is denoted by the symbol “Z”.
They do not have any fractional or decimal parts.
Integers include –
- Positive Integers: These are whole numbers greater than zero. Examples include 1, 2, 3, 4, and so on.
- Negative Integers: These are whole numbers less than zero. Examples include -1, -2, -3, -4, and so on.
- Zero: Zero is considered an integer but is neither positive nor negative.
Positive Integers can be classified as Prime Numbers and Composite Numbers.
- Prime Numbers –
  - A number other than 1 which does not have any factor apart from one and itself is called a prime number.
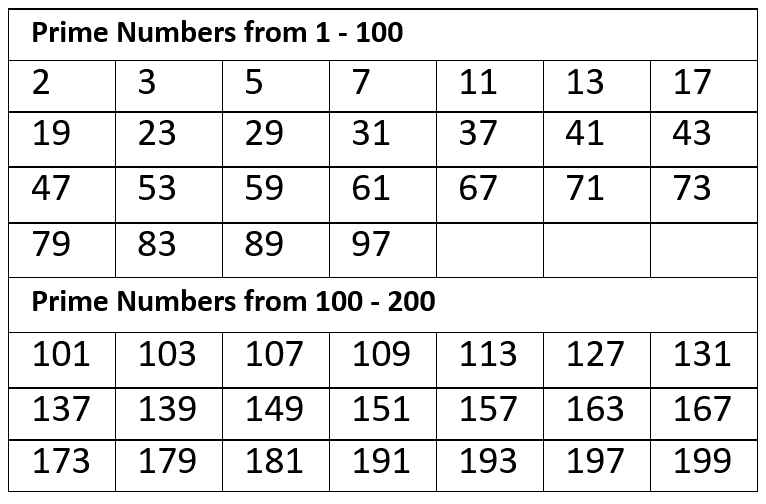
  - Examples for prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, etc.
  - Every prime number greater than 3 can be written in the form of (6k+1) or (6k 1) where k is an integer. $ \\ $
- Composite Numbers –
- Any natural number which has more than two factors is a composite number. In other words, a composite number is a number which has factors besides one and itself.
- Examples for composite numbers are 4, 6, 8, 9, 10, 14, 15, etc.
NOTE: The number 1 is neither prime nor composite. The only prime number that is even is 2.
There are 15 prime numbers between 1 and 50 and 10 prime numbers between 50 and 100. So, there are a total of 25 prime numbers between 1 and 100.
Even and Odd numbers –
- Numbers divisible by 2 are called even numbers whereas numbers that are not divisible by 2 are called odd numbers.
- Examples for even numbers are 2, 4, 6, 8, 10, etc. Examples for odd numbers are 1, 3, 5, 7, 9, etc.
Important Points relating to Even and Odd Numbers –
- Every even number ends in 0, 2, 4, 6 or 8.
- The sum of any number of even numbers is always even.
- The sum of odd number of odd numbers (i.e., the sum of 3 odd numbers, the sum of 5 odd numbers, etc.) is always odd.
- The sum of even number of odd numbers (i.e., the sum of 2 odd numbers, the sum of 4 odd numbers, etc.) is always even.
- The product of any number of odd numbers is always odd.
- The product of any number of numbers where there is at least one even number is even.
Perfect Numbers –
- A number is said to be a perfect number if the sum of all its factors excluding itself (but including 1) is equal to the number itself.
- For example, 6 is a perfect number because the factors of 6, l.e., 1, 2 and 3 add up to the number 6 itself.
- Other examples of perfect numbers are 28, 496, 8128, etc.

2. Hierarchy of Arithmetic Operations

The hierarchy of arithmetic operations are given by a rule called BODMAS rule.
The operations have to be carried out in the order in which they appear in the word BODMAS, where different letters of the word BODMAS stand for the following operations:
- B – Brackets
- O – Of
- D – Division
- M – Multiplication
- A – Addition
- S – Subtraction
There are four types of brackets:
- Vinculum: This is represented by a bar on the top of the numbers. For example, $ 2+3- \overline{4+3} $; Here, the figures under the vinculum have to be calculated as 4 + 3 first and the “minus” sign before 4 is applicable to 7. Thus the given expression is equal to 2+ 3-7 which is equal to -2.
- Simple Brackets: These are represented by ()
- Curly Brackets: These are represented by {}
- Square Brackets: These are represented by []
- The brackets in an expression have to be opened in the order of vinculum, simple brackets, curly brackets and square brackets, i.e., [{() } ] to be opened from inside outwards.

3. Factors, Multiples and Co-primes

Factors –
- If one number divides a second number exactly, then the first number is said to be a factor of the second number. Factors are also called sub-multiples or divisors.
- For example, 6 is a factor of 12; 3 is a factor of 21.
Multiples –
- If one number is divisible exactly by a second number, then the first number is said to be a multiple of the second number.
- For example, 12 is a multiple of 6; 24 is a multiple of 3.
Co-Primes –
- Two numbers are said to be relative primes or co-primes if they do not have any common factor other than 1.
- For example, the numbers 17 and 16 do not have any common factors and hence they are relative primes.
- None of the two numbers may individually be prime and still they can be relative primes.
- Unity is a relative prime to all numbers.

4. Rules for divisibility

Divisibility by 2 –
- A number divisible by 2 will have an even number as its last digit.
- For example : 732, 98746, 78, etc.
Divisibility by 3 –
- A number is divisible by 3 if the sum of its digits is a multiple of 3.
- For example, take the number 213, the sum of the digits is 2+1+3 = 6 which is a multiple of 3. Hence, the given number 213 is divisible by 3.
Divisibility by 4 –
- A number is divisible by 4 if the number formed with its last two digits is divisible by 4.
- For example, if we take the number 8536, the last two digits form 36. Since this number 36 is divisible by 4. the number 8536 is divisible by 4.
Divisibility by 5 –
- A number is divisible by 5 if its last digit is 5 or zero.
- For example: 1525, 90, 7650, etc.
Divisibility by 6 –
- A number is divisible by 6 if it is divisible both by 2 and 3.
- For example: 18, 42, 96, etc.
Divisibility by 7 –
- If the difference between the number of tens in the number and twice the units digit is divisible by 7, then the given number is divisible by 7. Otherwise, it is not divisible by 7.
- Take the units digit of the number, double it and subtract this figure from the remaining part of the number. If the result so obtained is divisible by 7, then the original number is divisible by 7. If that result is not divisible by 7, then the number is not divisible by 7.
- For example, let us take the number 595. The units digit is 5 and when it is doubled, we get 10. The remaining part of the number is 59. If 10 (which is the units digit doubled) is subtracted from 59 we get 49. Since this result 49 is divisible by 7, the original number 595 is also divisible by 7.
Divisibility by 8 –
- A number is divisible by 8, if the number formed by the last 3 digits of the number is divisible by 8.
- For example, the number 3816 is divisible by 8 because the last three digits form the number 816, which is divisible by 8. Similarly, the numbers 14328, 18864 etc. are divisible by 8. If we take the number 48764, it is not divisible by 8 because the last three digits number 764 Is not divisible by 8.
Note: In general, if the number formed by the last n digits of a number is divisible by 2ⁿ, the number is divisible by 2ⁿ.
Divisibility by 9 –
- A number is divisible by 9 if the sum of its digits is a multiple of 9.
- For example, if we take the number 792, the sum of the digits of this number is 7+9+2 which is 18. Since this sum 18 is a multiple of 9, the number 792 is divisible by 9.
Divisibility by 10 –
- A number divisible by 10 should end in zero.
- For example: 680, 72820, 5790, etc.
Divisibility by 11 –
- A number is divisible by 11 if the sum of the alternate digits is the same or they differ by multiples of 11 – that is, the difference between the sum of digits in odd places in the number and the sum of the digits in the even places in the number should be equal to zero or a multiple of 11.
- For example, if we take the number 785345, the sum of the digits in odd places is 16 and the sum of the digits in even places is also 16. Since these two sums are equal, the given number is divisible by 11.
Divisibility by 12, 14, 15 –
- Divisibility by numbers like 12, 14, 15 can be checked out by taking factors of the number which are relatively prime and checking the divisibility of the given number by each of the factors.
- For example, a number is divisible by 12 if it is divisible both by 3 and 4.
Divisibility by 19 –
- If the sum of the number of tens in the number and twice the units digit is divisible by 19, then the given number is divisible by 19. Otherwise it is not.
- Take the units digit of the number, double it and add this figure to the remaining part of the number. If the result so obtained is divisible by 19, then the original number is divisible by 19. If that result is not divisible by 19. then the number is not divisible by 19.
- For example, if we take 969, doubling the units digit gives 18 which when added to 96 gives a result of 114. Since 114 is divisible by 19, the number 969 is divisible by 19.

5. Factors and Co-Primes of a Number

Number of Factors of a Number

If N is a composite number such that N $ = a^p \cdot b^q \cdot c^r ….. $ where a, b, c are prime factors of N and p, q, r…. are positive integers, then the number of factors of N is given by the expression $$ (p+1) (q+1) (r+1)…. $$
- For example : $ 140 = 2^2 \times 5^1 \times 7^1 $. Hence 140 has $ (2+1)(1+1)((1+1) = 12 \ factors $.
Please note that the figure arrived at by using the above formula includes 1 and the given number N also as factors. So if you want to find the number of factors the given number has excluding 1 and the number itself, we find out (p+1)(q+1)(r+1) and then subtract 2 from that figure.
- In the above example, the number 140 has 10 factors excluding 1 and itself.

Number of ways of expressing a given number as a product of two factors

The given number N (which can be written as equal to $ a^p \cdot b^q \cdot c^r ….. $ where a, b, c are prime factors of N and p, q, r …… are positive integers) can be expressed as the product of two factors in different ways.
The number of ways in which this can be done is given by the expression- $$\frac{1}{2} {(p+1)(q+1)(r+1)…..} $$
- For Example : 140 can be expressed as a product of two factors in $ \frac{12}{2} $ or 6 ways (because (p+1)(q+1)(r+1) in the case of 140 is equal to 12.

6. Factors and Multiples of two or more Numbers

Least Common Multiple (LCM) and Highest Common Factor (HCF)

Least Common Multiple (LCM) –
- The LCM of two or more numbers is the least number which is divisible by each of these numbers (i.e. leaves no remainder, or remainder is zero).
- It is the expression of the lowest dimension which is divisible by each of them i.e. leaves no remainder, or remainder is zero.”
Highest Common Factor (HCF) –
- The HCF is the largest factor of two or more given numbers.
- It is the expression of highest dimension which divides each of them without remainder.
- HCF is also called GCD (Greatest Common Divisor).
Important Points –
- Product of two numbers = LCM × HCF
- LCM is a multiple of HCF
- LCM and HCF can each be found by either one of two methods:
  - Factorization
  - Division $ \\ $ $ \\ $
LCM by Factorization –
- Resolve the numbers into prime factors. Then multiply the product of all the prime factors of the first number by those prime factors of the second number, which are not common to the prime factors of the first number.
- This product is then multiplied by those prime factors of the third number, which are not common to the prime factors of the first two numbers.
- In this manner, all the given numbers have to be dealt with and the last product will be the required LCM.
- For Example : in order to find the LCM of 144, 504 and 720 we write each number in terms of its prime factors. $ \\144 = 3^2 \times 2^4$ $ \\ 504 = 3^2 \times 2^3 \times 7^1 $ $ \\ 720 = 2^4 \times 3^2 \times 5^1 $ $ \\ LCM \ is \ 24 \times 32 \times 7 \times 5 = 5040 $ $ \\ $ $ \\ $
LCM by Division –
- Select any one prime factor common to at least two of the given numbers. Write the given numbers in a line and divide them by the above prime number. Write down the quotient for every number under the number itself.
- If any of the numbers is not divisible by the prime factor selected, write the number as it is in the line of quotients.
- Repeat this process for the line of quotients until you get a line of quotients, which are prime to each other (i.e., no two “quotients” should have a common factor).
- The product of all the divisors and the numbers in the last line will be the required LCM.
- For Example : in order to find the LCM of 16, 9, 49 $ \\ $ $ \\ $ Thus, LCM = $ 2^3 \times 3^2 \times 1 = 72 $ $ \\ $ $ \\ $
HCF by Factorization –
- Resolve the given number into prime factors.
- The product of the prime factors common to all the numbers will be the required HCF.
- For Example : in order to find the HCF of 324, 576 and 784, first of all we resolve all the numbers into their prime factors $ 324 = 3^4 \times 2^2 \\ 576 =3^ 2 \times 2^6 \\ 784 = 7^2 \times 2^4 $ Then take the product of the factors common to all the numbers. HCF here will be $ 224 $. $ \\ $ $ \\ $
HCF by Long Division –
- Take two numbers. Divide the greater by the smaller, then divide the divisor by the remainder, divide the divisor of this division by the next remainder and so on until the remainder is zero.
- The last divisor is the HCF of the two numbers taken.
- In case of 3 numbers, by the same method find the HCF of any 2 numbers and then find the HCF of this HCF and the third number. This will be the HCF of the three numbers.
- For Example in order to find the HCF of 242 and 34 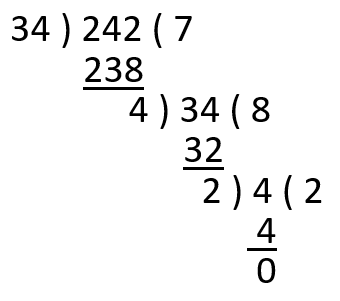$ \\ $ $ \\ $ Hence HCF of 242 and 34 is 2.

LCM and HCF Examples

Example 1: Find the smallest number which when divided by 5 or 8, leaves a remainder of 2 in each case and the number being greater than the two divisors. $ \\ $ The LCM of 5 and 8 is 40. Hence the required number is $ 40+2 = 42 $ $ \\ $ $ \\ $
Example 2: Find the smallest number which when divided by 19 and 23 leaves remainders of 13 and 17 respectively. $ \\ $ The LCM of 19 and 23 is 437. The difference between the divisor and the remainder in each case is the same i.e. (19-17 = 6) and (23-17 = 6). Hence, the number that satisfies the given conditions will be equal to $ 437-6=431 $. $ \\ $ $ \\ $
Example 3: Find the largest number with which when 425 and 373 are divided, respective remainders of 2 and 4 are left. $\\ $ Since 425 when divided by the number gives a remainder of 2 it means (425-2 = 423) is exactly divisible by that number. Similarly (373-4 = 369) is also exactly divisible by that number. Thus, the required number is $ HCF \ of \ (369, 423) = 9 $. $ \\ $ $ \\ $
Example 4: Find the largest number with which when 472, 832 and 1372 are divided, the remainders are the same. $ \\ $ Take the difference between any two numbers out of the three given numbers $ \\ 832-472 = 360 \\ 1372-832 = 540 $ The required number is the HCF of these two differences i.e., $ HCF \ of \ (360, 540) = 180 $.

7. Factorial

Factorial is first defined for positive integers. It is denoted by or “!”. Thus “Factorial n” is written as “n!”.
Factorial “n!” is defined the product of all the integers from 1 to n.
Thus $ n! =1 \times 2 \times 3 ….. (n-1) \times n $.
0! is defined to be equal 1.
0!=1 and, 1! is also equal to 1.
Factorials of 1 to 10 :-
- $ 1! = 1 $
- $ 2! = 2 $
- $ 3! = 6 $
- $ 4! = 24 $
- $ 5! = 120 $
- $ 6! = 720 $
- $ 7! = 5040 $
- $ 8! = 40320 $
- $ 9! = 362880 $
- $ 10! = 3628800 $

8. The Last digit of any Power

The last digits of the powers of any number follow a cyclic pattern i.e., they repeat after certain number of steps.
If we find out after how many steps the last digit of the powers of a number repeat, then we can find out the last digit of any power of any number.
For Example : Powers of 2 exhibit a pattern in their last digits.
- The last digit of 2¹ is 2.
- The last digit of 2² is 4.
- The last digit of 2³ is 8.
- The last digit of 2⁴ is 6.
- The sequence then repeats: the last digit of 2⁵ is the same as that of 2¹, and so on.
- The last digit repeats every 4 steps for the powers of 2. Therefore, if the power is a multiple of 4, the last digit will be the same as the last digit of 2⁴.
- In order to find the last digit of 2⁶⁷, find the nearest multiple of 4 less than or equal to 67, which is 64. Thus, the last digit of 2⁶⁷ will be the same as the last digit of 2³, which is 8.
Similarly, we can find the power cycle of all other numbers.

Last Digit of a Sum or Product

In general, when we want to find out the last digit of the sum of two numbers, we can just take the last digit of the two numbers and add them up. That will be the last digit of the sum.
Similarly, the last digit of a product will be equal to the last digit of the product of the last digits of the two given numbers.

You can also refer following videos to grasp basics of percentage in more details

Practice

Refer Topic: Ratio and Proportion: https://www.learntheta.com/placement-aptitude-permutation-combination/

Refer more Aptitude Questions with Solutions on Numbers: https://www.learntheta.com/aptitude-questions-numbers/

Practice Aptitude Questions on Numbers with LearnTheta’s AI Practice Platform: https://www.learntheta.com/placement-aptitude/