Aptitude Questions on Mensuration
Review Mensuration Concepts and Formulas
Q. 1 A rectangular garden has a fence around it, where the total length of the fence measures 60 cm. Interestingly, the length of this garden is exactly twice its breadth. Calculate the area of this rectangle?
A) 100 cm²
B) 150 cm²
C) 200 cm²
D) 300 cm²
Check Solution
Ans: C) 200 cm²
Let the breadth be bbb and the length be 2b
Perimeter = 2(l+b)=60
2(2b+b)=60
6b=60
b=10 , l=20
Area = $l \times b = 20 \times 10 = 200$ cm².
Q. 2 A perfectly round lake has a radius of 7 cm. Inside this lake, Mohan wants to construct the largest possible square platform that fits entirely within its boundaries. What is the area of this square platform?
A) 49 cm²
B) 98 cm²
C) 196 cm²
D) 294 cm²
Check Solution
Ans: B) 98 cm²
The diagonal of the square equals the diameter of the circle, 2r=14 cm.
Diagonal of the square = $\sqrt{2} \times \text{side}$,
Side = $\frac{\text{diagonal}}{\sqrt{2}} = \frac{14}{\sqrt{2}} = 7\sqrt{2}$
Area = $\text{side}^2 = (7\sqrt{2})^2 = 98$ cm².
Q. 3 An equilateral triangular park‘ where‘s each side measures exactly 10 cm. The park is known for its unique symmetry. What is the total area of this triangular park?
A) $25\sqrt{3}$ cm²
B) $50\sqrt{3}$ cm²
C) $75\sqrt{3}$ cm²
D) $100\sqrt{3}$ cm²
Check Solution
Ans: A) $25\sqrt{3}$ cm²
Area of an equilateral triangle = $\frac{\sqrt{3}}{4} \times \text{side}^2$
Area = $\frac{\sqrt{3}}{4} \times 10^2 = \frac{\sqrt{3}}{4} \times 100 = 25\sqrt{3}$ cm².
Q. 4 A triangular flag has a base of 12 cm and a height of 9 cm. The same amount of fabric is used to make a rectangular banner. If the length of this rectangle is 6 cm, can you determine its breadth?
A) 9 cm
B) 12 cm
C) 18 cm
D) 24 cm
Check Solution
Ans: A) 9 cm
Area of the triangle = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 12 \times 9 = 54$ cm².
Area of the rectangle = $\text{length} \times \text{breadth}$
$6 \times \text{breadth} = 54$
$\frac{54}{6} = 9$ cm.
Q. 5 A cylindrical closed container, used to hold water, has a radius of 7 cm and a height of 10 cm. Taking into account both the curved surface and the circular ends, can you calculate the total surface area of this cylinder?
A) 440 cm²
B) 660 cm²
C) 748 cm²
D) 960 cm²
Check Solution
Ans: C) 748 cm²
Total Surface Area = $2\pi r(h + r)$
=$2 \times \frac{22}{7} \times 7 \times (10 + 7) = 2 \times 22 \times 17 = 748$ cm².
Q. 6 A square-shaped field and a circular track have the same perimeter. If the side of the square is 28 cm, what would be the radius of the circular track?
A) 14 cm
B) 17.5 cm
C) 28 cm
D) 35 cm
Check Solution
Ans: B) 21 cm
Perimeter of square = $4 \times \text{side} = 4 \times 28 = 112$ cm.
Perimeter of circle = $2\pi r = 112$
$r = \frac{112}{2\pi} = \frac{112}{2 \times \frac{22}{7}} = 17.5$ cm.
Q. 7 A conical tent is being constructed, and its base has a radius of 3 cm while its height is 4 cm. Can you calculate the slant height of the cone?
A) 4 cm
B) 5 cm
C) 6 cm
D) 7 cm
Check Solution
Ans: B) 5 cm
Slant height = $\sqrt{\text{radius}^2 + \text{height}^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5$ cm.
Q. 8 A spherical decoration has volume of 904.78 cm³. Find its radius? (Take $\pi = 3.14$)
A) 6 cm
B) 7 cm
C) 8 cm
D) 9 cm
Check Solution
Ans: B) 7 cm
Volume of a sphere = $\frac{4}{3}\pi r^3$
$\frac{4}{3} \times 3.14 \times r^3 = 904.78$
$r^3 = \frac{904.78 \times 3}{4 \times 3.14} = 7^3$
r=7 cm.
Q. 9 Two similar triangular paintings are hung side by side, and their areas are in the ratio 16:25. What would be the ratio of the lengths of their corresponding sides?
A) 4:5
B) 16:25
C) 5:4
D) 64:125
Check Solution
Ans: A) 4:5
The ratio of the sides of similar triangles is the square root of the ratio of their areas.
$\sqrt{\frac{16}{25}} = \frac{4}{5}$
Q. 10 A semi-circular window has an area of 154 cm². If we assume π = 3.14, can you calculate the diameter of this window?
A) 7 cm
B) 14 cm
C) 28 cm
D) 56 cm
Check Solution
Ans: B) 14 cm
Area of semicircle = $\frac{1}{2}\pi r^2$
$\frac{1}{2} \times 3.14 \times r^2 = 154$
$r^2 = \frac{154 \times 2}{3.14} = 98$
$r = \sqrt{98} = 7 cm
Diameter = $2 \times r = 14$ cm.
Q. 11 A cube is painted on all its faces and then cut into smaller cubes of equal size. If the edge of the smaller cube is 1/3rd of the original cube, how many smaller cubes have exactly one face painted?
A) 54
B) 27
C) 36
D) 48
Check Solution
Ans: A) 54
If the cube’s edge is divided into 3 equal parts, the number of smaller cubes is $3^3 = 27$. The smaller cubes with exactly one face painted are those in the center of each face. Each face has $1^2 = 1$ such cube. Since there are 6 faces: $6 \times 1 = 6$
Q. 12 A cylindrical water tank has a diameter of 7 m and a height of 14 m. What is the volume of water it can hold?
A) 1078 m³
B) 539 m³
C) 1540 m³
D) 308 m³
Check Solution
Ans: B) 539 m³
Volume of a cylinder = $\pi r^2 h$, where $\frac{\text{diameter}}{2} = 3.5$ m and h=14 m.
V= $\pi \times (3.5)^2 \times 14 = \frac{22}{7} \times 12.25 \times 14 = 539 \, \text{m}^3$
Q. 13 A decorative cone has a slant height of 13 cm and a base radius of 5 cm. Including both the curved surface and the base, what is the total surface area of this cone?
A) 220 cm²
B) 230 cm²
C) 240 cm²
D) 260 cm²
Check Solution
Ans: D) 260 cm²
Total Surface Area of a cone = $\pi r (r + l)$, where r=5 cm and l=13 cm.
$\text{TSA} = \pi \times 5 \times (5 + 13) = \frac{22}{7} \times 5 \times 18 = 282.86 \, \text{cm}^2$
Q. 14 The diagonal of a rectangular billboard is 25 cm, and one of its sides measures 15 cm. What is the total area of this rectangular billboard?
A) 300 cm²
B) 400 cm²
C) 375 cm²
D) 450 cm²
Check Solution
Ans: A) 300 cm²
Using Pythagoras theorem, $\text{Diagonal}^2 = \text{Length}^2 + \text{Breadth}^2$ :
$25^2 = 15^2 + \text{Breadth}^2 \implies \text{Breadth} = 20 \, \text{cm}$
Area = $15 \times 20 = 300 \, \text{cm}^2$
Q. 15 A smooth, shiny sphere has a diameter of 12 cm. Can you determine the total surface area of this sphere?
A) 452.16 cm²
B) 314 cm²
C) 272 cm²
D) 432 cm²
Check Solution
Ans: A) 452.16 cm²
Surface Area of a sphere = $\pi r^2$, where $r = \frac{\text{diameter}}{2} = 6$ cm.
$\text{Surface Area} = 4 \times \pi \times 6^2 = 4 \times \frac{22}{7} \times 36 = 452.16 \, \text{cm}^2$
Q. 16 The area of an equilateral triangle is 36√3 cm². Find its side length.
A) 6 cm
B) 12 cm
C) 9 cm
D) 8 cm
Check Solution
Ans: B) 12 cm
Area of an equilateral triangle = $(\sqrt{3}/4) a^2$. Let side length be a :
$36\sqrt{3} = (\sqrt{3}/4) a^2 \implies a^2 = 144 \implies a = 12 \, \text{cm}$
Q. 17 A cylindrical vessel of radius 7 cm is filled with water to a height of 10 cm. If the water is poured into a cuboidal vessel of base area 154 cm², find the height to which the water rises.
A) 6 cm
B) 10 cm
C) 5 cm
D) 8 cm
Check Solution
Ans: B) 10 cm
Volume of water = Volume of cylinder = $\pi r^2 h = \frac{22}{7} \times 7^2 \times 10 = 1540 \, \text{cm}^3$
Height in cuboid = Volume/Base Area = $1540 / 154 = 10 \, \text{cm}$
Q. 18 An octahedron, a unique 3D shape with eight triangular faces, is being studied. How many edges does this geometric solid have?
A) 12
B) 8
C) 6
D) 24
Check Solution
Ans: A) 12
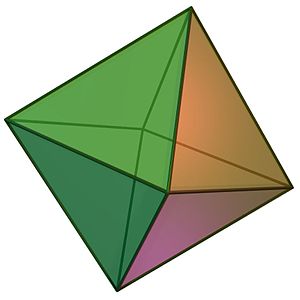
A regular octahedron has 8 triangular faces, 6 vertices, and 12 edges.
Q. 19 The length, breadth, and height of a cuboid are in the ratio 1:2:3, and the total surface area of the cuboid is 88 m². Find the volume of this cuboid:
A) 48 m³
B) 64 m³
C) 72 m³
D) 84 m³
Check Solution
Ans: A) 48 m³
Let dimensions be x,2x,3x. Total surface area:
$2(x \cdot 2x + 2x \cdot 3x + 3x \cdot x) = 88 \implies x^2 = 4 \implies x = 2$
Volume = $x \cdot 2x \cdot 3x = 2 \cdot 4 \cdot 6 = 48 \, \text{m}^3$
Q. 20 A hollow hemispher bow has an outer radius of 10 cm and a wall thickness of 2 cm. What is the total volume of this hollow hemisphere?
A) 2640 cm³
B) 2688 cm³
C) 2600 cm³
D) 2800 cm³
Check Solution
Ans: B) 2688 cm³
Volume of hemisphere = $(2/3) \pi (R^3 – r^3)$ , where R=10, r=8:
V=$\frac{2}{3} \pi (10^3 – 8^3) = \frac{2}{3} \cdot \frac{22}{7} (1000 – 512) = 2688 \, \text{cm}^3$
Refer Topic wise Aptitude Questions with Solutions
Refer Questions for next topic: https://www.learntheta.com/aptitude-questions-statistics/